Про принципи вибору гвинтів на моделях літаків

На сьогоднішній день існує омана щодо вибору гвинта на моделях хобійно-пілотажного профілю (в тому числі і тренувальні моделі). Причина в тому, що за традиційно-спортивними напрямками давно вироблені орієнтири і проведені теоретичні обгрунтування оптимального вибору гвинтів: в швидкісних, гоночних, таймерних моделях. Тому спробуємо прийти до правильних критеріїв.
На перший погляд все просто. Береш зовнішню і дросельні характеристики мотора та сімейство аеродинамічних характеристик наявних у продажу гвинтів, за останніми будуєш сімейство графіків потрібної потужності в тих самих координатах, що і зовнішні характеристики мотора. Тоді в бажаному швидкісному режимі знаходиш перетин графіків — ось і отримав оптимальний гвинт.
У житті все складніше. Якщо при належній працьовитості зовнішні характеристики мотора ще можна зняти на стенді, то продувочні характеристики модельних гвинтів — це навряд чи. Модельні фірми, навіть гранди, їх теж не дають.
Вихід напрошується такий: за базові параметри приймаються загальноприйняті або рекомендовані виробником мотора, а далі йде їх послідовне наближення в потрібну конструктору сторону. Для цього треба хоча б якісно розуміти, як ті чи інші конструктивні параметри впливають на характеристики гвинта.
Трохи з теорії гвинта
Почнемо все ж з основних положень теорії гвинта, взявши з неї лише кілька формул:
Тяга гвинта P=α*p*n2*D4
Потужність, потрібна на обертання гвинта T=β*ρ*n3*D5
Відносна хода гвинта λ=V/(n*D)
ККД гвинта η=(α*λ)/β
Навантаження на гвинт B=(8/π)*(P/(ρ*V2*D2))
Тут:
α — коефіцієнт тяги гвинта
β — коефіцієнт потужності гвинта
ρ — щільність повітря
n — оберти гвинта
D — діаметр гвинта
V — швидкість літака.
Аналітично тут багато не нарахуєш, тому що головне, це як поводяться коефіцієнти тяги і потужності гвинта, а також їхнє відношення, яке визначає ККД гвинта. Ці параметри встановлюються емпірично шляхом зняття продувкою в аеродинамічній трубі характеристик конкретних гвинтів. Тому ми розглянемо їх якісну зміну в залежності від різних параметрів. Почнемо з ККД. Для типового гвинта графік η=f(λ) виглядає так:
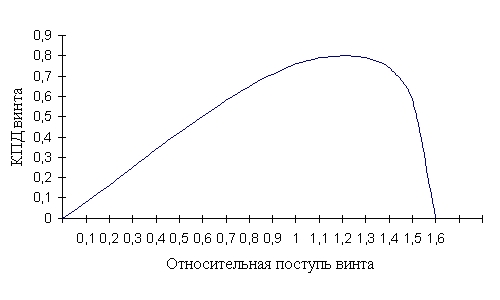
Зверніть увагу, відносний поступ — величина безрозмірна і дорівнює одиниці при швидкості польоту 1 м/сек, обертах гвинта 60 об/хв і його діаметрі 1 метр.
Тепер треба пояснити, чому графік виглядає так. При нульовій ході ККД дорівнює нулю, тому що гвинт не робить ніякої роботи — літак стоїть на місці. При ході 1,6 даний гвинт також не робить роботи, тому що його крок такий, що лопаті рухаються з нульовим кутом атаки (тобто перпендикулярно потоку) і не утворюють ніякої тяги.
Для гвинтів з іншим кроком загальний вигляд графіка такий же, але він пропорційно стиснутий (при меншому кроці) або розтягнутий (при більшому кроці) по осі. При ковзанні 20-30% (для даного гвинта в області λ = 1,1-1,4) ККД гвинта максимальний і може досягати значення 0,8. Це найбільш вигідна область з точки зору використання потужності двигуна.
Цікаво, що в цій галузі ККД змінюється незначно, тобто при зниженні швидкості в цьому діапазоні тяга пропорційно зростає, що позитивно позначається на стійкості польоту по швидкості. При ковзанні менше 15-20% ККД починає різко падати, тому що кут атаки лопаті знижується, відповідно падає Cy лопаті гвинта і знижується його тяга. В діапазоні відносної ходи від 0 до 0,9 ККД гвинта майже лінійно залежить від швидкості, що вказує на майже незмінну його тягу!!!
Тобто всупереч розхожій думці, тягу правильно підібраного гвинта в польоті можна досить точно визначити по статичній тязі з невеликими поправками.
Якщо точніше подивитися на цю частину графіка, то він кілька опуклий в лівій половині. Це відбувається тому, що тяга гвинта трохи зменшується при зниженні швидкості внаслідок збільшення навантаження на гвинт B (див. формулу, там швидкість в знаменнику, та ще й в квадраті). Типова залежність η/η0=f(B) при зміні B від нуля до 10 виглядає так:
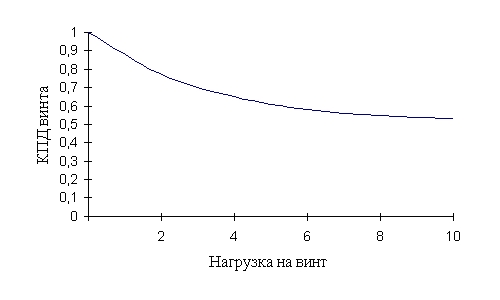
Падіння коефіцієнта тяги пов'язане зі зміною характеру потоку повітря перед гвинтом при зниженні швидкості. Але нам важлива не причина, а те, що правильно підібраний гвинт в статиці дає тягу, меншу тяги при максимумі ККД, не більше ніж на 15%.
Підбір гвинта
Тепер про те, що таке правильно підібраний гвинт. Повернемося до графіку ККД. Якщо на ньому нанести сімейство графіків гвинтів, що розрізняються тільки кроком, то вони будуть нагадувати наявний, але стислий, або розтягнутий по осі λ, як це згадувалося вище. Правда, максимум ККД при зменшенні кроку теж зменшується. Значення максимуму 0,8 має місце в разі, якщо оптимальне ковзання гвинта потрапляє на відносну ходу величиною близько одиниці. Це і є один з критеріїв правильно підібраного гвинта.
Щоб оцінити, де знаходяться типові значення візьмемо мотор 40-го об'єму з потужністю 1,3 к. с. при 14000 обертах на хвилину і порахуємо типовий для цього випадку гвинт розміру 250 на 150. При пілотажній швидкості 90 км/год отримуємо λ рівним 0,43. При такій ході максимальний ККД не перевищить 0,6. Щоб отримати такий ККД крок гвинта при ковзанні 20% має становити близько 9 сантиметрів, а для реалізації потужності з таким кроком діаметр гвинта треба збільшити до 27-30 сантиметрів. З зазначеним вище кроком ККД буде не вище 0,5. Такий низький ККД досягається за рахунок занадто високих обертів двигуна на максимальній потужності.
Подивимося, як виглядають у світлі вище сказаного професіонали F3A. Переважна їх більшість літають на OS MAX 140 RX з гвинтом 16 на 14 дюймів на швидкостях 90-70 км/год при обертах мотора близько 9000. 14-ти дюймовий гвинт оптимальний при 25% ковзанні на швидкості близько 180 км/год. При 90 км/год його ККД складе 0,65, а при 70 км/год — 0,5.

Простий розрахунок показує, що в діапазоні швидкостей 50-100 км/год тяга цього гвинта взагалі від швидкості не залежить, а визначається тільки обертами мотора. Напевно саме це подобається професіоналам, так як з даним гвинтом в пілотажному діапазоні швидкостей існує взаємно однозначний зв'язок між становищем ручки газу і тягою мотора. Оптимальний же гвинт розміром 18 на 8 дюймів дасть тягу, більшу відсотків на двадцять при 90 км/год, але вона буде залежати не тільки від обертів мотора, але й від швидкості літака. Профі згодні пожертвувати цією добавкою заради кращої керованості тягою.
Найгірше становище у таймерних моделей. Там мотор крутить до 30000 обертів в хвилину, а швидкість підйому літака маленька. При дуже маленькому діаметрі гвинта навантаження на гвинт виходить моторошним. В контексті сказаного дуже правдоподібно звучить зауваження Є. Вербицького, згадане в 5 номері МСіХ за 1999 рік. Там сказано, що за його розрахунками «звичайні повітряні гвинти F1C діаметром 180 мм на частоті обертання 28000 об/хв мають ефективність близько 40%. Шляхом зниження обертів до 7000 за допомогою редуктора при одночасному збільшенні діаметра повітряного гвинта можна збільшити ККД гвинта до 80%». Такі ж результати вийшли у автора цього матеріалу.
Ось у радіогонок — там як раз навпаки. Там швидкості такі, що майже під будь-які оберти можна розрахувати гвинт з ККД близьким до 0,8. Вище мало уваги приділялося коефіцієнту потужності β. Це не випадково. Справа в тому, що даний параметр важливий при розрахунках екстремального режиму. Якщо гвинт розрахований на максимум тяги при максимумі потужності, то на часткових режимах, про які йшлося в основному, є впевненість що потужності двигуна вистачить. Причому незалежно від зовнішньої характеристики двигуна, тому що оберти в формулі потрібної потужності стоять третього ступеня T=β*ρ*n3*D5. Так швидко потужність не може падати зі зниженням обертів навіть у двигунів з резонансним вихлопом і швидкісними фазами газорозподілу. Для пілотажних моделей важливіше не екстремальні режими, а весь діапазон швидкостей і навантажень на гвинт.
Кілька рядків про ширину лопаті. Широко поширена думка, що зменшуючи ширину лопаті гвинта можна трохи підвищити його ККД. Це дійсно так, але для швидкісних режимів з відносно невеликим навантаженням на гвинт. Для гвинта з вузькою лопаттю характеристика η/η0=f(B) йде більш круто. Настільки, що на великому навантаженні ККД гвинта з більш широкою лопаттю виходить вище. Разом з тим, це відбувається в області малих абсолютних значень ККД.
Для низьких швидкостей польоту при високообертних моторах знижувати крок і збільшувати діаметр гвинта можна не безмежно. При куті атаки лопаті, меншому найвигіднішого по полярі даного профілю, тяга одиничного елемента знижується швидше, ніж зростає площа гвинта. Тобто для повільного польоту є мінімальний крок, далі якого оптимізація гвинтокорилої установки можлива виключно через редуктор.
Які з вище зазначених розлогих міркувань можна зробити висновки?
1. Правильно підібраний гвинт забезпечить пілотажці приблизно постійну максимальну тягу в широкому діапазоні швидкостей польоту, починаючи від старту.
2. Існуючі модельні двигуни через швидкісні зовнішні характеристики не дозволяють на повільному пілотажі сучасних тенденцій F3A використовувати гвинти з хорошим ККД.
3. Для сучасного 3D-пілотажу і на літаках типу фан-флай перспективним можна вважати застосування мотор-редуктора з різко збільшеним діаметром гвинта. Тільки цей шлях дозволить різко (удвічі) поліпшити співвідношення тяга/вага мотоустановки. Тоді можна розраховувати на великий запас тяги на вертолітних швидкостях і висінні. Зараз на Diamante висять з гвинтами 310 на 95 мм. Це межа, нижче знижувати крок вже неефективно.

І останнє — про гвинти змінного кроку. На моделях пілотажного типу їх застосування недоцільно. ВІШ, звичайно, дозволить на малих швидкостях дати приріст тяги за рахунок більш високого ККД, але цей приріст там не потрібен. До того ж цей приріст буде менше теоретичного через аеродинамічну крутку лопаті. На відміну від вертолітних гвинтів, у літакових пристойна крутка, оптимальна тільки на одному кроці. У великій авіації ВІШ набув поширення в основному для забезпечення високої економічності мотоустановки, що для моделей ролі не грає.
P.S. У матеріалі наведено формули і графіки з монографій Олександрова В.Л. «Повітряні гвинти» і Болонкіна А.А. «Теорія польоту літаючих моделей». У розрахунках ККД використовувалася сітка аеродинамічних характеристик англійського гвинта з останньої роботи.





















































